APPARENT LACK OF SYMMETRY IN STELLAR 

ABERRATION AND EUCLIDEAN SPACE TIME

ABSTRACT :-

The effect of stellar aberration seems to be one of the simplest phenomena in astronomical observations. But there is a large literature about it betraying a problem of asymmetry between observer motion and source motion. This paper addresses the problem from the point of view of Euclidean space-time, arising from the proposition that stellar aberration (or Bradley aberration) gives rise to a Lorentz expansion.

( 1) INTRODUCTION:-

It is known that the earth completes a full circumference around the Sun every year. Consequently, since the Earth-Sun radius (R_e) is well known, it is easy to determine the earth tangential velocity (V_t) required to complete the circumference in twelve months (T seconds). We have:

2 p (R_e) =(V_t)T       [equation 4]

Equation (4) predicts that the average translational velocity V of the earth around the Sun is 29.79 Km/s. Of course, the earth velocity vector changes continuously in direction and completes a full cycle during a one year period while the earth circles the Sun.  

On Figure A [26], an observer on Earth detects the photons emitted by a stationary star S, located in a direction perpendicular to the Earth velocity V_t. The star is located at such a large distance from the earth that the parallax caused by the orbit diameter around the Sun is completely negligible. Only the transverse velocity matters here. The stationary star S is emitting photons in all directions. The Earth and the telescope are moving upward at a velocity V . The telescope must make an angle q with respect to the real direction of the arriving photons in order to collect them at its focus.

In astronomy textbooks, the relative velocity between photons (at velocity c) and the Earth (V_t), explains why a telescope on Earth (see Fig. A) must be pointing at the angle q , with respect to the Earth-star direction, to be able to point at the star. Figure A shows that while the photons move in straight line toward the Earth, they will always remain in the axis of an inclined telescope, since it is moving sideways with the Earth. The angle q is equal to:

Tan q =(V_t)/c        [EQUATIO N 5]

Equation (5) gives q equals 20.5 arc-s. This is in perfect agreement with the value of aberration observed so many times since Bradley[11] in 1727. During the year, the observed direction of the stars makes one oscillation with an amplitude of 20.5 arc-s., as expected from the Earth motion around the Earth. The value of 20.5 arc-s. is called the constant of stellar aberration. The equation (5) ,in fact, gives classical formula for aberration in absolute time in which the waves (strictly the normals of the wave fronts) are not subjected to aberration to the great disappointment of Fresnel [1]. The relativity theory has solved this problem in terms of the relativity of simultaneity. Equal aberration for light photons and light waves requires this revision of simultaneity concept. Aberration is understood as aberration of the wave front normals. Such an aberration is the corollary of the relative simultaneity. According to Born [27], the relativistic stellar aberration formula calculation with a wave-front normal or phase through Lorentz transformation turned out to be identical to that with a particle through Einstein’s composition rule for velocities. Consequently, formulas are derived either by the first method in text books [28-33], or by the second method in the text books [34-36]. Today, the aberration is formally derived in text-books [6-8] from the relativistic transformation of the phase. But in these text-books [6-8] and [28-33], in the derivation of aberration from the relativistic transformation of the phase, the inverse Lorentz transformation equations are used as if one is going from moving frame to the rest frame. The preceding statement becomes quite clear later on in Section 3 (Conclusion–2) where on substituting inverse Lorentz transformation in place of Lorentz transformation [equation (11)] in right hand side of equation (10) and on comparing the coefficients of x, y, z and t in the resulting equation, the relativistic stellar aberration formula is derived. Aberration can also be derived from relativistic composition law of velocities which when applied in moving frame of source, using inverse Lorentz Transformations, predicts an aberration effect produced by the motion of the source in rest frame as discussed below.

Consider an inertial rest frame K with respect to which another inertial frame K’ is moving with velocity v along x-axis in positive (+X) direction. Further, consider a light photon emitted by a light source at rest in frame K’ such that the direction of emission lies in x-y plane and makes an angle q and q’ with +Y- axis in frame K and K’ respectively. Using inverse Lorentz transformations, the velocity components c cos q and c sin q of light photon along Y and X-axis respectively in rest frame K are expressed in terms of velocity components (c cos q’) and (c sin q’) in K’ as

c sin q = (c sin q’ + v)/(1+v sin q’/c)     ------(1)

c cos q = (c cos q’)/g(1+v sin q’/c) where g = 1/(1-v²/c²)^0.5 ------(2)

Taking ratio of (1) and (2), we get

Tan q = g (c sin q’ + v)/(c cos q’)     ------(3)

The equation (3), derived using inverse Lorentz Transformation, predicts active aberration effect produced by the motion of source in rest frame K. This prediction is based on , relative motion between source and observer, which is claimed to be the cause of aberration even by Einstein [12] and Pauli [13]. But in the beginning of twentieth century, the observational evidence for the lack of longitudinal additions to the velocity of light by the radial motion of the source (Guthnick [14], desitter [15], Zurhellen[16]), later improved for extragalactic objects (Stromberg [17], Heckmann [18], Schmidt [19], Brecher [20], Barnet, Davis and Sanders [21]), convinced about the observational absence of active aberration. This absence was first tested by H. Seeliger [9] and Nyren [10] and also, recently, some authors [22-25] have shown this absence. This lack of observational confirmation of active aberration was interpreted as an error in the theory of relativity and as a hint that the latter had to be revised accordingly [2-5]. History forgot their [2-5] argument because they failed to provide correct explanation to the observed absence of active aberration. This revision of relativity theory is in the form of Euclidean Space –time in place of the Einstein’s four dimensional space time. Euclidean Space –time is such that both relativistic transformation of the phase and relativistic composition law of velocities make use of Lorentz transformations in deriving the relativistic aberration and doppler formulas. Further, the statement [1], that the aberration is a correction to be applied between observers in relative motion, is self-evident in the Euclidean Space-time

Moreover, the absence of active aberration leads to apparent lack of symmetry in aberration i.e. aberration is observed when observer is moving and not when source is moving. In order to find correct and rational explanation for the observed absence of active aberration produced by the motion of source, the mechanism of stellar aberration is reviewed in the next section.

(2) MECHANISM OF ABERRATION :

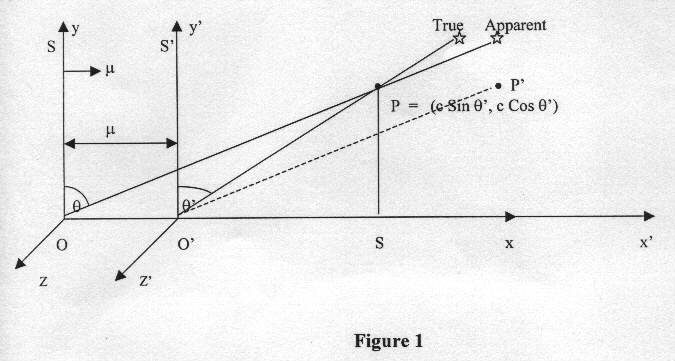
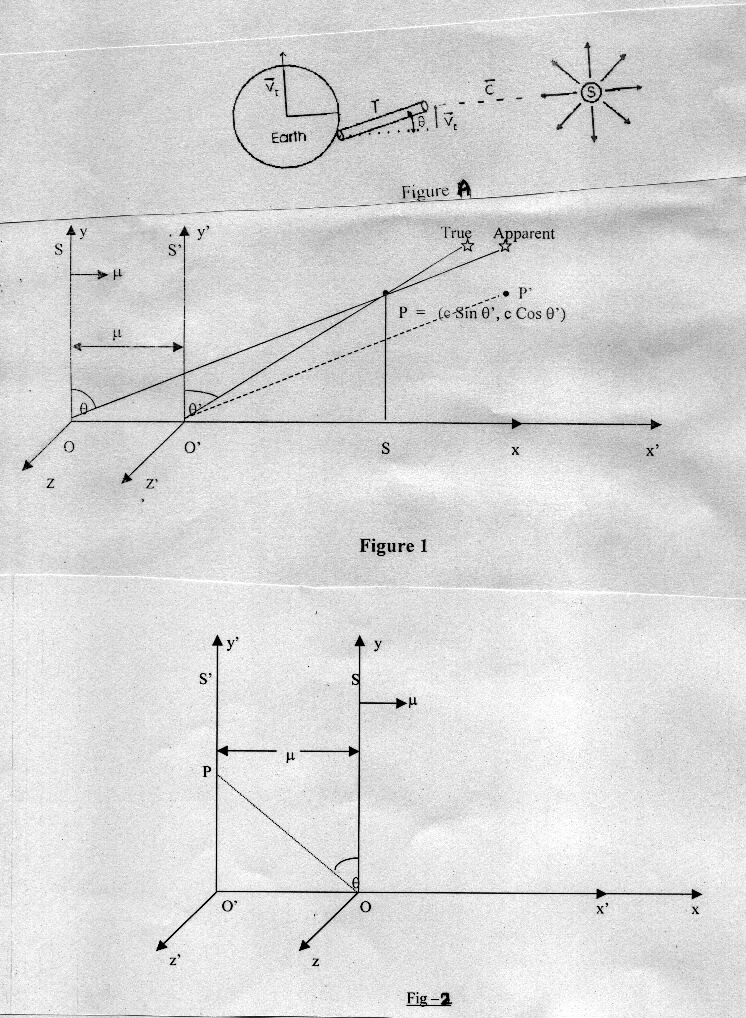
The aberration of star light is as follows. Let us assume that the rest frame S' of Fig. 1 is fixed by astronomical coordinates to the solar system, with respect to which the frame S attached to the Earth is moving towards right with orbital velocity m at time t' = -1 as shown in Fig.l. Consider a starlight photon in S' at point P in the x' - y' plane with x' and y' coordinates as c sin q' and c cos q', respectively. This photon would be observed simultaneously in S and S' when O and O' coincide at t = t' = 0. Due to stellar aberration [37] the observer O sees the incoming direction of the starlight photon along line O'P' at t = t' = 0 such that PP' = m and point P' coincides the point P at t' = -1. This coincidence of P and P' is possible only in classical time concept, t = t', and not in Einstein’s new time concept, t = b (t' + m x' / c²) where b = 1/ (1 - m²/c²)^0.5. The problem lies in the fact that the stellar aberration as outlined above can be explained only in classical time concept with which the principle of constancy of light speed in S and S' is incompatible. It is this incompatibility that lead Einstein to establish new time concept [38]. Our endeavour is to find a time concept that explains stellar aberration as well as principle of constancy of light speed in S and S’.

In frame S this photon approaches the point O along the straight line OP which occupies the position O'P' in S' at t' = 0. But there is nothing worth moving length^*(In [39] Einstein defined the concept of moving length as “By means of stationary clocks set up in the stationary system and synchronizing in accordance with Einstein’s definition of simultaneity, the observer ascertains at what points of stationary system the two ends of the rod to be measured are located at a definite time. The distance between these two points, measured by the measuring rod already employed which in this case is at rest, is also a length which may be designated the length of the rod. The length to be discovered by the above operation, we will call the length of the (moving) rod in stationary system.) in Fig. 1 to substantiate the preceding statement. In objective reality there are only rest lengths OP and O'P' of S'. This means that the coinciding of O and O' at t = t' = 0 is accompanied by dislocation of initial point P of starlight photon to the point P' in S. In other words, the length OP at t' = -1 is a moving length which moves to position O'P' at t' = 0 in Fig. 1. But the principle of constancy of light speed in S and S' demands that the moving length OP must be Lorentz contracted along the direction of motion of S so that the rest length OP in S' reveals itself as a dilated value rather than a contracted value in S. Moreover, the dislocation of initial point P of starlight photon to point P' in S implies that the relativity of simultaneity acquires meaning only when the spatial and temporal axes coincide each other in S and S'.

In Fig.1 the angle q of tilt of the telescope to see the photon in the earth frame S can be obtained by considering the rest length OS of the frame S' as Lorentz contracted moving length of the earth frame S, and we get tan q = OS / PS = b (m + c sin q') / c cos q' where b = 1/ (1 - m²/c²)^0.5. This is the relativistic formula for the aberration of starlight which was already deduced by Einstein in his first paper [40].

The formula for the angle of aberration, instead of being tan q = m/c, then becomes sinq = m/c when q’ = 0. The relativistic formula agrees with the classical formula for quantities of first order in case of relative transverse velocity between star and earth. Further, Let assuming that Fig. 2 represents. Fig.1 at time instant t’ = +1 such that q’ = 0. Additionally, there is present at origin O of earth frame S a small horizontal plane mirror in x-z plane that reflects the incoming star light photon at  

t’ = t = 0. In accordance with laws of reflection the starlight photon is reflected at angle sin q = m / c along OP in earth frame S and at normal along O’P = c in frame S’ because of normal incidence in S’. After reflection the earth becomes moving source that has emitted reflected starlight photon at t = t’= 0. It is quite obvious that the direction OP of outgoing reflected starlight photon in earth frame S is apparent direction (as incoming starlight photon direction was apparent in S) and the direction O’P of outgoing reflected starlight photon in frame S’ is true direction. This implies that the earth frame S as moving source with transverse velocity emits the reflected star-light photon without any aberration. Consequently, the apparent lack of symmetry (described in section 1 of this paper) in stellar aberration, when the star is moving at transverse velocity, can be explained on the basis of above discussion. The fact, that Einstein’s theory fails to explain this lack of symmetry in aberration, implies that something is wrong with Einstein’s theory. Let us see what new conclusions can be drawn about relativity from the above discussion of stellar aberration that explains apparent lack of symmetry in aberration.

(3) CONCLUSION (1) :

The angle q of tilt of the telescope to see the photon in the earth frame S can be obtained by considering the rest length OS of the frame S' as Lorentz contracted moving length of the earth frame S, and we get tan q = OS / PS = b (m + c sinq ') / c cos q' where b = 1/ (1 - m²/c²)^0.5. This clearly establishes that the rest length OS in S' does reveal itself as a dilated value in moving frame S in Fig. 1 rather than a contracted value. Further, in Fig. 1 the point P is the origin of temporal axis O'P in S' and of temporal axis OP in S for the starlight photon at P. Due to stellar aberration the physical existence of these temporal axes in S and S' can be experimentally proved in the form of apparent and true star positions observed simultaneously in S and S' when O and O' coincide at t = t' = 0 and observe the starlight photon previously at point P. This implies that (a) the distinction between space and time disappears completely. (b) there is no difference between time direction [41] and space direction, (c) time should be measured in imaginary numbers rather than real ones. On this basis the conclusion that space time is Euclidean appears to be convincing and reasonable enough, since with imaginary time it has a Euclidean metric.

Moreover, the principle of relativity demands that the rest length in S must also reveal itself as a dilated value in S'. This is possible only when frame S also becomes Lorentz contracted along with frame S' when one moves from frame S' to moving frame S in Fig. 1. This implies that the length OO' = bm of frame S in Fig. 1 becomes Lorentz contracted as OO' = m in going from frame S' to S in Fig. 1. This reveals another aspect of Euclidean space time that when rest clock at O' registers  

t'=-1 in Fig. 1, the observer at O adjusts itself spatially as well as temporally on moving from S' to S so that the rest clock at O in S registers t = -1.

3. CONCLUSION (2)

In Euclidean space-time the relativistic transformation of the phase and relativistic composition law of velocities make use of Lorentz transformation in deriving the relativistic aberration and doppler formulas as discussed below.

In Fig. 1 the length OP of moving frame S in Euclidean-space time is calculated as

OP = [OS² + PS²] ^0.5

Substituting OS = b (m + c sin q’) and PS = c cos q’ in above equation, we get

OP = b (c + m sin q’)

This means that cosq in S is represented in Euclidean space-time as

cos q = (PS / OP) = (c cos q’)/ b (c + m sin q’)   ------(6)

Keeping in view the relativistic law of conservation of linear momentum, the linear momentum components along Y – axis of the starlight photon in frames S and S’ of Fig. 1 must be equal i.e.

(hw/2pc) cos q = (hw’/2pc) cos q’     ------(7)

Where h is planck’s constant and w, w’ are angular frequencies of starlight photon in S and S’ respectively. Rearranging terms in equation (7) and substituting equation (6) in (7), we get

w = bw’ (1+m cos q’/c)       ------(8)

The relation between wave-vectors k and k’ of starlight photon in frames S and S’ of Fig.1 can be found easily by substituting w = ck and w’=ck’ in equation (8) and we get

k = b k’ (1+m cos q’/c)      ------(9)

Consider a plane wave of frequency w’ and wave-vector k’ associated with the starlight photon in frame S’ of Fig.1. In moving frame S of Fig.1 due to linearity of Lorentz transformation this wave indeed remains a plane wave but will have, in general, a different frequency w and wave vector k but the phase f of the wave is an invariant quantity.

wt – k.r = f = w’ t’ – k’.r’      -------(10)

Where r and r’ are the radial motion vectors of starlight photon of Fig. 1 in frames S and S’ respectively.

If we substitute equations (8) and (9) in left hand side (wt – k.r) of equation (10) along with Lorentz transformation equations

x = b (x’ + mt’), y = y’, z = z’ and t = b (t’+mx’/c²)  -------(11)

we get right hand side (w’t’ – k’.r’) of equation (10). This verification of equation (10) leads to the result that the statement, for w and k in equation (8) and (9), that are derived on the basis of Euclidean space-time concept, represent angular frequency and wave-vector of starlight photon in moving frame S and are in accordance with Lorentz transformation equation. In fact, the equation (8) and (9) represent the relativistic doppler effect statements derived on the basis of Euclidean space-time concept. Moreover, the relativistic stellar aberration formula, derived in Section 3(1) of this paper using Euclidean space-time concept, also satisfies the Lorentz transformation equations (11).

Thus, the above discussion leads to the result that Euclidean space-time is such that both relativistic transformation of the phase and relativistic composition law of velocities make use of Lorentz transformation in deriving the relativistic aberration and doppler effect formulas.

(3) CONCLUSION (3)

It is stated in [1] that aberration is a correction to be applied between observers in relative motion. This statement is self-evident in Euclidean space-time concept as discussed below.

In Fig. 1, if the velocity m of frame S is allowed to take an arbitrary value between (-c) and (+c), the distance ( OO’ = m) is to be corrected for each observer at O in relative motion in order to find the apparent stellar position at angle q in Euclidean space-time. This obviously leads to the result [1] that aberration is a correction to be applied between observers in relative motion.

REFERENCES :

[1] D.-E. Liebscher, P.Brosche, Bonn, Aberration and relativity, Astron.Nachr.319 (1998).

[2] Hayn, A.N. (1920) : Didaktisches zur Aberration II, Astron.Nachr.212, 81-88 (5070).

[3] Tomaschek, R. (1925) : Uber die Aberration, Z.Physik 32, 397-402.

[4] Osten, H.(1925) : Aberration und Relativitat, Astron.Nachr.224, 66-67 (Nr.5356).

[5] Mohorovicic, St. (1928) : Optik bewegter Korper, in : E.Gehrke, Handbuch der physikalischen Optik 2, 917 ff., Leipzig, J.A. Barth.

[6] W. Pauli, Theory of Relativity, p.19 (Pergamon Press, Oxford, 1958)

[7] Robert Resnik, Introduction to Special Relativity, p.82 (Wiley Eastern Private Limited, New Delhi, First Edition 1962, Reprinted 1972).

[8] J.D. Jackson, Classical Electrodynamics, p.521 (Wiley Eastern Private Limited, New Delhi, Second Edition 1975, Reprinted 1989).

[9] Seeliger, H. 1884, Astron.Nachr. 109, 275-280 (2610).

[10] Nyren, M. (1888) : Zur Aberration der Fixsterne, Bull. Acad.Imp.St. Petersburg 32, 402-412.

[11] J. Bradley “Account of a New Discovered Motion of the Fixed Stars” Phil. Trans. 35p.637 (1728).

[12] Einstein, A. 1916, Uber spezielle und allgemeine Relativitatstheorie, Braunschweig, Vieweg.

[13] Pauli, W. 1921, Enzyklopadie der mathematischen Wissenschaften V/2, S.563.

[14] Guthnick, P.1913, Astron.Nachr. 195, 265-272 (4670).

[15] deSitter, W. 1913, Phys.Z. 14,429.

[16] Zurhellen, W.1914, Astron.Nachr.198, 1-10 (4729).

[17] Stromberg, G.1931, Publ.Astr.Soc.Pacific 43, 266.

[18] Heckmann, O. 1960, Ann. d' Astrophysique 23, 168-173.

[19] Schmidt, Th. 1964, Z.Astrophys. 60, 106-111.

[20] Brecher, K. 1977, Phys.Rev.Lett. 39, 1051-1054.

[21] Barnet, C., Davis, R., Sanders, W.L. 1985, Astrophys. J. 295, 24-27.

[22] H.E. Ives “Extrapolation from the Michelson-Morley Experiment” J.Opt. Soc. Am. 40, pp. 185-190 (1950).

[23] E. Eisner, “Aberration of Light from Binary Stars – a Paradox?” Am. J. Phys. 35, pp.817-819 (1967).

[24] T.E. Phipps “Relativity and Aberration,” Am. J. Phys., 57, pp., 549-550 (1989) also Phipps T.E., Jr., “Stellar Aberration from the standpoint of the Radiation Convection Hypothesis.” Phys. Essays 4, 368, (1991).

[25] H.C. Hayden, Stellar Aberration, “Galilean Electrodynamics, 4.pp. 89-92 (1993).

[26] Paul Marmet, Stellar Aberration and Einstein’s Relativity, Physics Essays, Vol. 9, No : 1p.96-99, 1976.

[27] Born, M. 1920, Die Relativitatstheorie Einsteins, Vieweg Verlag Braunschweig.

[28]  Bohm, D. 1965, The special theory of relativity, W.A. Benjamin.

[29] Joos, G. 1956, Lehrbuch der theoretischen Physik, Leipzig, Geest & Porting, 9.Aufl.

[30] Herlt, E., Salie, N. 1978, Spezielle Relativitatstheorie, Berlin, Akademie-Verlag.

[31] Sommerfeld, A. 1959, Vorlesungen, IV. Optik, 2. Aufl., Leipzing, Geest & Portig.

[32] Schneider, M. 1979, Himmelsmechanik, BI Mannheim.

[33a] Varicak 1910, Phys. Z.11, 93-96.

[33b] Varicak 1910, Phys. Z.11, 287-294.

[33c] Varicak 1910, Phys. Z.11, 586-587.

[34] Landau, L.D., Lifshic, E.M. 1962, Klassische Feldtheorie, Berlin, Akademie-Verlag 1964.

[35] Goenner, H. 1996, Einfuhrung in die spezielle and allgemeine Relativitatstheorie, Heidelberg, Spektrum AV.

[36] Rindler, W. 1986, Essential Relativity, Heidelberg, Springer.

[37] Albert B. Stewart, The Discovery of Stellar Aberration, Scientific American, p.100. (March, 1964).

[38] Harald Nordenson, Relativity, Time and Reality, p.84 (George Allen and Unwin Ltd., Ruskin House, Museum Street, London 1969).

[39] Albert Einstein, On the Electrodynamics of Moving Bodies, Ann. Physik, 17, 891 (1905).

[40] W. Pauli, Theory of Relativity, p.17 (Pergamon Press, Oxford, 1958).

[41] Stephen Hawking, A Brief History of Time, p.142, (Bantam Press Edition reprinted, 1996). 

Rajan Dogra, Instructor, Wireless Operator Trade Industrial Training Institute, Chandigarh.

Mail: House No. 3291, Sector 27-D,
Chandigarh - 160 019, India
Phone : 0091-172-650148
E-mail: rajandogra@mailcity.com

Author’s note:AS ONE GOES THROUGH MY PAPER THE FOLLOWING POINTS OF MISUNDERSTANDING ,CONFUSION AND PUZZLE ARE MOST LIKELY TO CROP UP IN ONE'S MIND.MY REJOINDER TO THESE POSSIBLE POINTS OF MISUNDERSTANDING AND CONFUSION IS ALSO STATED BELOW. (1.) The goal of this paper is to reconcile the experimental fact that the speed of light is identical in any inertial frame with the Newtonian concept of absolute time. It is clear that what the author attempts do to is like the quadrature of the circle, that is, it is impossible. MY REJOINDER :- >In my paper the statement "--The problem lies in the fact that the stellar aberration as outlined above can be explained only in classical time concept with which the principle of constancy of light speed in S and S' is incompatible --- " refutes the observation that the goal of my paper is to reconcile the experimental fact that the speed of light is identical in any inertial frame with the Newtonian concept of absolute time (read classical time concept). The observation that what the author attempts to do is like the quadrature of the circle, that is, it is impossible, and this impossibility is also stated in my paper when I state that the classical time concept and the principle of constancy of light speed in S and S' are incompatible. (2.) The special theory of relativity is built on the observed constancy of the speed of light.With the additional assumptions of homogeneity and isotropy of space and homogeneity of time, the Lorentz transformations, viz. the relations between the coordinates of space-time events in two different inertial frames, can be derived by purely mathematical deduction. Length contraction, time dilation {and the relativity of time} all are consequences of the Lorentz tranformations. One cannot have one and not the other. That is to say, one cannot have length contraction and also Newtonian time.It appears that the author is doing the same in his paper. However, the author is basing many of his arguments on contracted or dilated lengths without any reference to the context from which this concept originates. Moreover, one has to be careful about applying, e.g., the term "length contraction". In the usage of special relativity it means that the length of a meter stick at rest if measured from a moving system { at a specified time in the moving system} will be contracted. In contrast, the author is using "length contraction" in a very haphazard way.One is puzzled by what exactly the author has in mind when he speaks of the``Euclidean nature of space-time''. He states that ``... time should be measured in imaginary numbers...." If so, then a Euclidean nature of space-time implies that the sace-time interval squared is invariant, i.e., has the same value in any inertial frame. However,the space-time interval squared whose invariance expresses the constancy of the speed of light in special relativity , has, as mentioned above, the Lorentz transformations as inescapable consequence and,therefore, forces one to abandon Newtonian absolute time. If the author wants to find an alternative to special relativity that is compatible with Newtonian time, then he has to set up an alternative to the Lorentz transformation from system S to system S', such that the speed of light is invariant and t= t'. This is like the quadrature of the circle. MY REJOINDER :-In my paper the statement "--But the principle of Constancy of light speed in S and S' demands That the moving length OP must be Lorentz Contracted ---" clearly reveals that my arguments on contracted or dilated lengths originates from the concept of special theory of relativity of which the principle of constancy of light speed in any inertial frame is first postulate. The only point of difference between my arguments and special theory of relativity is the concept of moving length. In my arguments I am describing the path followed by starlight photon in earth frame S as moving length whereas the usage of special relativity describes the length of a moving materialistic object as moving length. My description of moving length is substantiated by the derivation of the relativistic stellar aberration formula on the basis of my description of moving length. Further, my description of moving length leads to coinciding of the spatial and temporal axes something unheard in usage of special relativity. This coincidence of spatial and temporal axes means that two points on X-axis having spatial separation equal to c ( i.e. the speed of light in vacuum) are not at same time instant but are having temporal separation of one second. This is what I meant by Euclidean nature of space-time. In this Euclidean nature of space-time the special theory of relativity encompassing the principle of constancy of light speed in any inertial frame still holds good along with Lorentz transformations and consequences flowing from these transformations (viz length contraction, time dilation, etc.) In this context the statement of my paper, that the rest length OS in S' reveals itself as a dilated value rather than a contracted value in S, is nothing but time dilation because the rest length divided by light speed in vacuum denotes temporal separation in Euclidean Nature of space-time.Further, the invariance of space-time interval squared has got no meaning in Euclidean Nature of space-time because the space and time are on same footing in Euclidean space-time. The another consequence of Euclidean space -time is that time is indistinguishable from directions in space, i.e. if one can go east, one can turn around and head west; equally if one can forward in time, one ought to be able to turn around and go backward because spatial and temporal axes coincide each other in Euclidean space - time. This means that the spatial adjustment of observer O in last sentence of my paper is equivalent to temporal adjustment when one moves from S' to S. (3)Please draw a Minkowskian plane (looks(!) like a Euclidean plane) with horizontal axis x and vertical axis t. Let Z=(0,0) S=(1,2) E=(0,4)Mark these points in the diagram and then connect (with straight lines) ZE (along the t-axis), ZS and SE so that you get a triangle. Using the Minkowski metric (ds^2 = dx^2 - dt^2)(Euclidean: ds^2 = dx^2 + dt^2 ), please calculate the "Minkowski Length" of the lines ZE, ZS and SE and convince yourself that ZE > ZS + SE (and post the solution !?). Of course, the cat is out of the bag: you will have noticed that you're only solving the twin "paradox".ZE is the worldline of the twin "at home", while ZS + SE is the worldline of the intrepid traveller from Z (earth at 00:00 hours) to S (star) and back to E (earth at the end). The travel speed is obvious, or is it ?? (If this is too boring, please prove that ZE is the LONGEST possible path from Z to E; reminder: Z-to-E MUST be timelike throughout !)MY REJOINDER:-Euclidean plane is not like Minkowskian plane because Euclidean space-time is to be drawn with horizontal x-axis and horizontal t-axis coinciding each other.This means that two points on x-axis having spatial separation equal to light speed 'c' in vacuum are not at same time instant but are having temporal separation equal to one second. Consequently, When Z = (0,0) and S = (1,1) ,then Z and S are on x-axis but at different time instants in Euclidean space-time. When intrepid traveller starts from Z with travel speed equal to half of light speed , also assume that a light photon also starts from Z towards star S. When traveller reaches star S =(1,3) ,the light photon reaches at P = (2,2) on x-axis. In Euclidean space-time the path SP followed by photon on x-axis is moving length that is transversed by the star S to reach the intrepid traveller in the frame of traveller. Therefore, the point P =(2,2) indicates initial star position in traveller 's frame. Accordingly,the Euclidean length should be calculated by joining Z and P and not Z and S . Therefore, The Euclidean length ZP is equal to time like length (0,2) that elapsed at Z in forward journey of intrepid traveller. Same argument is applicable to backward journey. Tell me what you think of the given experimental proof of Euclidean nature of Space- time. Send me your mail to E-mail: rajandogra@mailcity.com

Mathematical Contradiction of Special Relativity (By Eric J. Lange) and Euclidean Space -Time

Einstein based his special theory of relativity on two postulates:

1. The laws of physics are the same in all inertial systems (reference frames that move uniformly and without rotation). There are no preferred inertial systems. When a certain reference-frame moves with constant speed with respect to another, processes of nature will obey the same laws of physics in either reference-frame.

2. The speed of light in vacuum has the same constant value c in all inertial systems.

Let a light signal travels along X-axis with speed c in rest frame C such that  x = ct

The same light signal travels, according to Einstein, also with respect to reference-frame C' with a speed equal to c. With respect to C' the equation for the movement of the light signal becomes: x'= ct '

The movement of frame C' with respect to frame C is described by: a = v t

(For the three equations above and all still to derive, applies that C' coincides with C at t = 0 and t' = 0. The covered distances x and x' of the light signal are at that moment also equal to zero.)

Einstein had to make concessions in relation to absolute time which was generally accepted back then. Because distances x and x' (for t>0) were obviously not equal, t and t' had to be different too.

x = ct

x' = c t'

x' < x

c' = c

t' < t

The result of Einstein's principle of the constancy of the speed of light, was therefore that the course of time in C and C' had to be different. A clock would run slower in C' than in C.

The following derivation of the Lorentz-transformation according to the special theory of relativity, is probably the most frequently occurring version of the derivation of the transformation-equations that can be found in the literature^{1, 2}. It is this version that is taught on universities around the world.

The light signal moves uniformly rectilinear with respect to both reference-frames. This means there exists a linear relation between coordinates x, y, z, t and x', y', z', t'. The most common form of this relation is as follows: